Implementing automata in hardware

The nature of today's digital hardware

At the time of writing - in the year 2000 - most widely available computer hardware is essentially two dimensional.

By this I mean that the technology involves etching circuitry onto flat, two-dimensional wafers of silicon.

Sometimes more than one layer can be etched, but generally speaking, excursions into the third dimension do not get very far.

Implementing N-dimensional automata in M-dimensional substrates

Efficiently implementing an N-dimensional cellular automata in hardware should prove simple provided that the hardware itself has N dimensions or higher.

Today, in practice this means that it is possible to simulate relatively large one- and two-dimensional automata without significant loss of update speed.

However, when three-dimensional automata are simulated, the distance between adjacent cells must rise as the size of the automata rises - as there are simply not enough dimensions to accomodate the desired connections.

As more and more cells are added, adjacent cells in the automata must move to locations which become unboundedly distant from one another in the hardware.

Exploiting the substrate's potential

For many applications, it is desirable for the automata to be of the same dimensionality as the hardware in order to best exploit the available connectivity.

This is often true of applications which simulate universal computation, or perform other processing tasks, such as encryption or generating pseudo-random numbers.

Use of (for example) a one-dimensional automata in a two-dimensional computing substrate can result in a waste of the available interconnect resources.

Periodic boundary conditions

There's an important exception to the idea that it is usually desirable to simulate an N-dimensional automata in N-dimensional hardware.

If the automata has periodic boundary conditions, then you may get a performance increase by moving to N + 1 dimensions.

  • One dimension

    Here's an image of a one-dimensional automata in a one dimensional substrate without periodic boundary conditions.

    The cells are represented by black dots, or "nodes".

    Here's an image of a one-dimensional automata in a two-dimensional substrate with periodic boundary conditions present:

    Here's one attempt at implementing this in one dimension:

    Although the space occupied by each node remains the same as in the first example, the distance between neighbouring nodes has doubled. If signal propagation times are significant his may result in virtually halving of the automata's update speed.

    Another attempt, again with the same physical "spacing" between the nodes:

    This is an even more dramatic failure.

    The slowest pair of neighbours is the limiting factor in the updfate rate of the entire automata. If the update rate depends at all on the distance between neighbouring cells, the large distance between the first and last cell will cause the automata to update very slowly.

  • Two dimensions

    Here is a comparison between two two-dimensional automata - identical in all respects, except that one is flat, while the other has had toroidal "wrap-around" applied to it.

    Without wrap-around With wrap-around
    		     

    The colours and numbers are intended to help visualise the relationship between cells in the two automata.

    Note the diagram indicates the most efficient way of organising the cells in an essentially two dimensional plane.

    Individual cells are portrayed as taking up the same area in both diagrams.

    Note that wrap around effectively forces neighbouring cells apart from one another.

    More wiring is needed to connect the cells, and the wires have to cross over one another to reach their neighbouring cells. As both wires and crossovers take up area, this forces the cells further apart, requiring yet more wiring.

If the speed of update of the automata depends at all on the time taken for signals to propagate to neighbouring cells, the larger maximum distance between neighbours will cause delays, and slow down the global update rate.

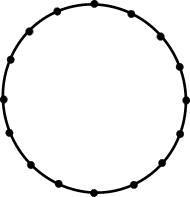
Embedding two-dimensional automata in three-dimensional substrates

Lastly, here's an image of a two-dimensional automata with periodic boundary conditions. It is represented as a torus embedded in a three dimensional space:

It will be seen that even if extra dimensions are available, toroidal wrap-around still has some adverse effect on update speed.

This can be seen by observing that the distance between nodes on the "outside" of the torus is larger than the corresponding distance on the inside.

Assuming the cells on the "inside" are as closely packed as possible, those on the "outside" must be sub-optimally packed, with more distance between them than is strictly needed.

While topological transformations may be able to reduce this effect to a small value, the delay can't be completely eliminated.

Summing up

Use of periodic boundary conditions is not well in tune with the spirit of using cellular automata as a model for rapid computation in hardware.

If you are trying to best exploit the available connectivity - by using an automata with the same dimensionality as your substrate - periodic boundary conditions are worth taking some effort to avoid.

Tim Tyler | tim@tt1.org | http://cell-auto.com/