Automata whose inverses have unboundedly large neighbourhoodsInvertible automataThere are a number of techniques designed to create cellular automata which are reversible and have corresponding inverse automata associated with them.Generally speaking most of these techniques made it easy to find the inverse automata. This is true of Fredkin's method, the use of partitioning schemes, techniques involving embedding a irreversible automata in a higher-dimensional space and the guarded context technique.
Cryptographic applicationFor some cryptographic applications, it is desirable to have an operation whose inverse is computationally hard to compute. Such functions are called "one-way" functions. There are also "one-way trap-door" functions - functions whose inverse is difficult to identify, but relatively easy to calculate once it has been located.With this goal in mind, some pre-requisites for they type of system needed should be clear: If the "radius" of an automaton's inverse is relatively small, it will be possible to identify its inverse by considering a small space surrounding the cell whose inverse function is needed and apply brute force search techniques to locate the inverse function for that cell. If such a technique succeeds, finding the inverse is unlikely to prove much of a problem. In order to make finding an inverse function for a particular cell difficult, it is desirable to make the domain of the inverse function include a very large number of cells. Ideally, it should be a function of all the other cells in the automaton. This would be likely to make a brute force as hard as possible.
The existence of "one-way" automataThe existence of such automata was proven by Jarkko Kari in a paper called "Reversibility of 2D Cellular Automata is Undecidable" [Kari, 1990]. He showed that for a class of reversible automata using the VN neighbourhood, in general, no bound may be placed on the size of the neighbourhood required by their inverse automata.He also showed that there is no finite effective procedure for locating the inverse of such a reversible automaton, i.e. there is no general algorithm for finding the inverse rule with a time complexity bounded by a computable function.
Constructing automata whose inverses have unboundedly large neighbourhoodsThe construction presented here can be applied to generate automata of any number of dimensions. If working in more than one dimension, the resulting automata are typically spatially non-uniform.The method involves making a one dimensional path through every cell the automaton, and constructing the rules of the cells around that. The inverse function can be computed only by traversing the path in a specified direction - and performing a long string of calculations in series.
ExampleIn order to explain the procedure, we will present an example using a one-dimensional automaton.This automaton will be based on Wolfram's rule-30.
Rule-30's update rule is:
The new update rule is essentially: This looks identical, except the "i"s on the right hand side of the equation have all had one added to them.
The rule is applied to a finite field, without the use of periodic boundary
conditions
When
The resulting automata displays much the same behaviour as rule-30 would if it was skewed sideways. However - unlike Rule-30 when applied to a finite field, it is reversible - and an inverse automata exists.
To calculate the inverse, start with the cell at
Since at that point
Next, consider the cell at
This is the inverse function at
Next, consider the cell at
This is the inverse function at The last series of steps can be applied iteratively, resulting in the unambiguous recovery of the entire state of the automaton at the previous time step.
Two dimensionsIn order to apply this proceedure to a two dimensional automata, first a path through the plane must be decided upon.
 One end of the path is nominated as the starting cell. The state of each cell in the following generation depends only on the state of neighboring cells in the previous generation. In addition, cells which are further away from the starting cell than the current position cannot be considered.
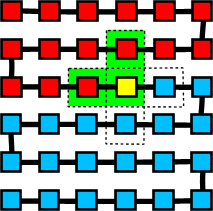 In this diagram, the yellow cell is the current cell. The red cells are nearer the starting cell. The dotted lines indicate the VN-neighbourhood. The green colour indicates the cells which may contribute to the update function of the yellow cell. The update function may be any boolean function, with one restriction: no matter what the states of the "red" cells are, the yellow cell must have the "final say" - and should always be able to completely influence the state of the cell in the next generation. In practice, this menas that the yellow cell should be Exclusive OR'd with the function contributed by the red cells. As Exclusive OR is a linear function, this has sometimes resulted in this type of automata being referred to as "quasi-linear".
Iterating in either directionIterating "forwards" is simply a case of applying the transformation in each cell, like a normal cellular automata. This operation may performed in parallel.When iterating "backwards", the state of each cell must be calculated in a series of steps along the path, starting with the first cell on the path, and progressing along it.
Use of two passesThe result of updating an automata using the resulting rule is that the state of each cell depends only on earlier cells along the path.If it is desirable to have each cell depending on the state of every other cell in the automaton, it is necessary to traverse the path twice, once in each direction.
NotesAn extension of this construction to half-infinite domains and uniform automata is possible. This appears to indicate that the Margulis/Toffoli "Conjecture 8.1" in [Margulis and Toffoli, 1990] - which conjectures that all invertible automata are structurally invertible - i.e., can be (isomorphically) expressed in spacetime as a uniform composition of finite invertible logic primitives - should be treated with caution when considering this type of system.There are other results along similar lines. Richardson is said to have proved that if a cellular automata is invertible, then its inverse is a cellular automata [Margulis and Toffoli, 1990]. I feel obliged to add that this is not true if the automaton is non-uniform, or if the automaton is half-infinite, with a single edge. Similar comments apply to Max Garzon's Corollorary 7.15: "If T is one-one then T-1 [i.e. T's inverse] [...] is defined by a local transformation." [Garzon, 1995]
Construction techniques for composite reversible automataModifications to the techniqueA page listing some ways of modifying the technique is available here.ReferencesKari J.: "Reversibility of 2D Cellular Automata is Undecidable", 1990;Margulis, N. H., and Toffoli, T.: "Invertible Cellular Automata: A Review", 1990; |