Wolfram numbersDue to his contributions to their study in the early 1980s, the 1D, r=1, k=2 automata seem to have become associated with the name of Stephen Wolfram.Consequently the family of the 256 "elementary" cellular automata have come to be known as "Wolfram rules", and the numbers associated with each rule are now often known as "Wolfram numbers". The Wolfram numbering scheme for his simple cellular automata is described in his 1983 paper, "Statistical Mechanics of Cellular Automata". This paper has been reprinted in the book of his collected papers, entitled "Cellular Automata and Complexity" (Addison Wesley, 1994).
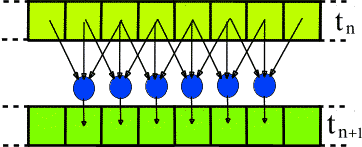
Essentially the idea is to find the states corresponding to neigbourhoods containing
For example, the rule described by:
Illustration of how the number of rule 30 is derived from its behaviour:
|